How experimentalists calculate the mass of a new particle?
(Examples using Excel)
It is interesting to see what quantities experimentalists measure in a detector and how they use them to obtain different parameters, as the mass of a new particle, the momentum and energy of non seen neutral particles, that permits to identify them... These calculations may be quite lengthy using a calculator, but can be made more easily and quickly using a spreadsheet and its capabilities (pasting formulas...).
We shall show examples using bubble chambers pictures. But the same principles apply in other detectors (wires detectors...).
Here is a presentation of bubble chambers.
The necessary relations are :
- Conservation of momentum : 
- Relativistic expression of kinetic energy:
(using c=1)
Some applications :
1) electron-positron annihilation. Consider a basic application of the preceding. Feynman diagrams can be sometimes misleading, Although e+e- --> g is the basic vertex for electromagnetism interactions, e+ e- cannot in fact annihilate in one photon, but at least in two. Do you know why? answer
2) Simple event. A simple application to see how the equations apply. K8K0 event. Picture. Excel worksheet
3) Missing momentum energy in K- p collision,How to use the data to deduce that some particles are non-seen in the final state. Picture Excel worksheet.
4) Discovery of the Omega- particle. A more complicated, but interesting example, the discovery of Omega- particle.
The Omega- particle belongs to the spin 3/2+ baryon decuplet. In 1963, nine of the particles of this decuplet were known, but Gell-Mann, on the basis of the quark model, predicted the existence of a tenth, with strangeness -3 (its composition is in fact sss). The Omega- was discovered in a bubble chamber in Brookhaven in 1964, and it was a great success for the quark model.
Calculate the mass of this famous particle using the experimental data. The
bubble chamber picture of this event is here.
The data for the momenta of each track related to this event are given in polar
coordinates :
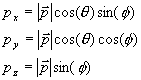
q is in fact Azimuth, and f is dip.
|
Track number |
Azimuth in degrees |
Dip in degrees |
Momentum in MeV/c |
|
1 (incoming K-) |
4.2 |
1 |
4890 |
|
2 (K+) |
6.9 |
3.3 |
501 |
|
3 (W-) |
14.5 |
-1.5 |
|
|
4 (p- from
kink) |
79.5 |
-2.7 |
281 |
|
5 (p- from
L0) |
344.5 |
-12 |
256 |
|
6 (p from L0) |
9.6 |
-2.5 |
1500 |
|
7 (g on right) |
357 |
3.9 |
82 |
|
8 (g on left)) |
63.3 |
-2.4 |
177 |
Repeated use of momentum conservation laws and energy relation permit to reconstruct all the steps of this event, and to calculate the mass of the W-. To help you, here are the equations of all reactions :
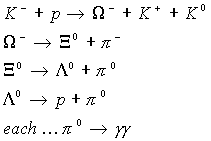
a) First, you have to convert these data in Cartesian coordinates, in order to be able to use conservation laws.
b) Then, first step : calculate the mass of the particle that decays in 7 and 8 photons, and deduce which particle it is.
c)
Calculate the mass of the neutral particle that decays in
5 and 6 (
and a proton)
d)
Calculate the momentum and energy of 
(which decays in 
and 
) and deduce its mass.
e)
Calculate the mass of the 
particle (that decays in 
and 
)
f)
The 
in the first reaction is a neutral particle that is non-seen
in bubble chamber. You can do a check of consistency, calculate its mass and
verify it corresponds tho the known one.